【人気ダウンロード!】 三角 関数 角度 求め 方 161057-三角関数 角度 求め方
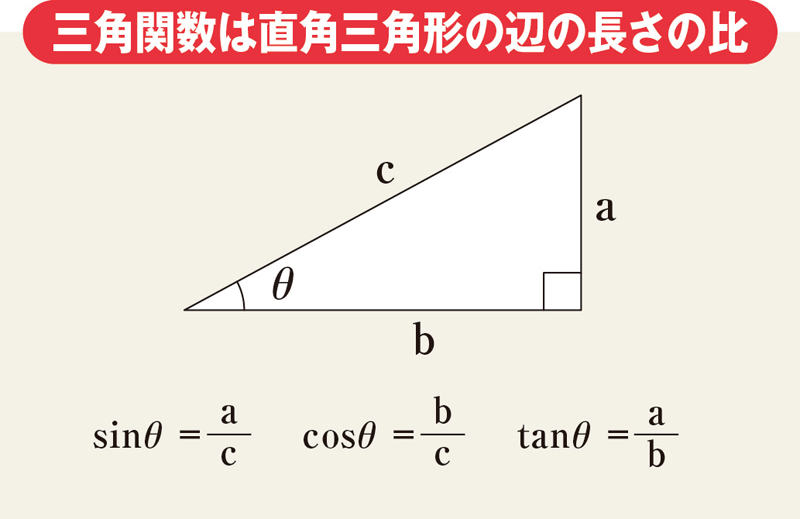
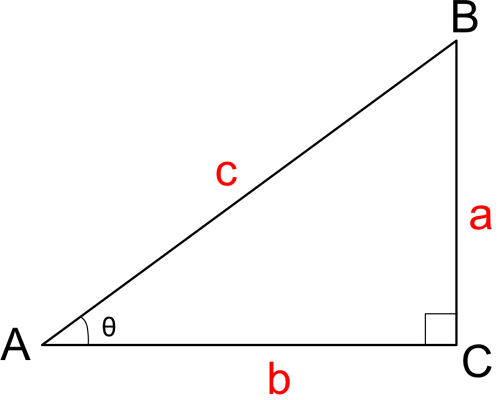
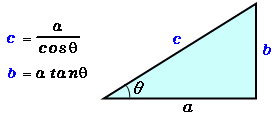
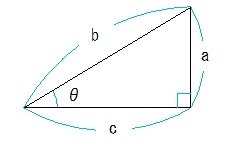
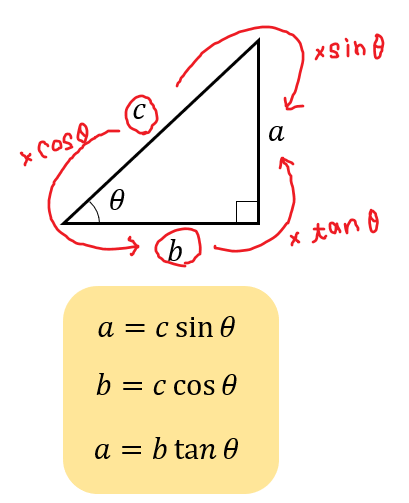
三角形の3辺の長さから角度を求める 三角形の記号 使用する記号ですが、図のように、三辺の長さを\( a,b,c \)、角度を\(A,B,C\)で表すことにします。 角度は、次の2段階のステップで求めます。 求める角度の余弦(cos(コサイン))を求める。この問題を見て,逆三角関数 tan1 (C言語では atan() や atan2()) を使って CP と CQ の角度をそれぞれ求め, 両者を比較しようと考えた方が多いのではないでしょうか. しかしこの問題では,角度そのものではなく角度差の符号を求めればよいので, 逆三角関数を使う方法よりも簡単で優れた,外積 サイン (sin)、コサイン (cos)、タンジェント (tan)の計算をする前に、三角関数の基本をおさらいしておきましょう。 直角三角形の3辺 a、b、c は、以下のような関係にあります。 例えば、辺cの長さが5で、角度θが30°だった場合、辺aの長さは以下のようになります。 例
家電やスマホに必須 三角関数は陰の働き者 中高数学おさらい 三角関数 数列 文系でも怖くない 学び直し 数学 ダイヤモンド オンライン
三角関数 角度 求め方
三角関数 角度 求め方-三角形の証明・形状問題 → 携帯版は別頁 三角関数の合成公式 a sin θb cos θ の形の式は一つの三角関数にまとめることができます.これを三角関数の合成公式といいます. a sin θb cos θ= √a2b2√nnnnni sin (θα) (ただし, α は cos α=Fig 1 CORDICアルゴリズムで必要な直角三角形群と変換ベクトルの絶対値 さて,続いて,実際に与えられた角度の三角関数を計算する方法について述べる.具体的な角度があった方がいいので,ここはθ=30°とする.また,説明を簡単にするため,ここでは



三角比と三角関数 高校物理をあきらめる前に 高校物理をあきらめる前に
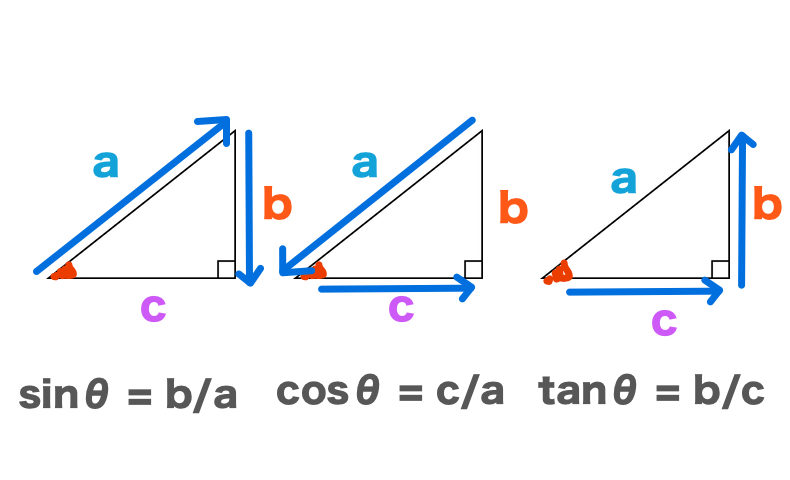
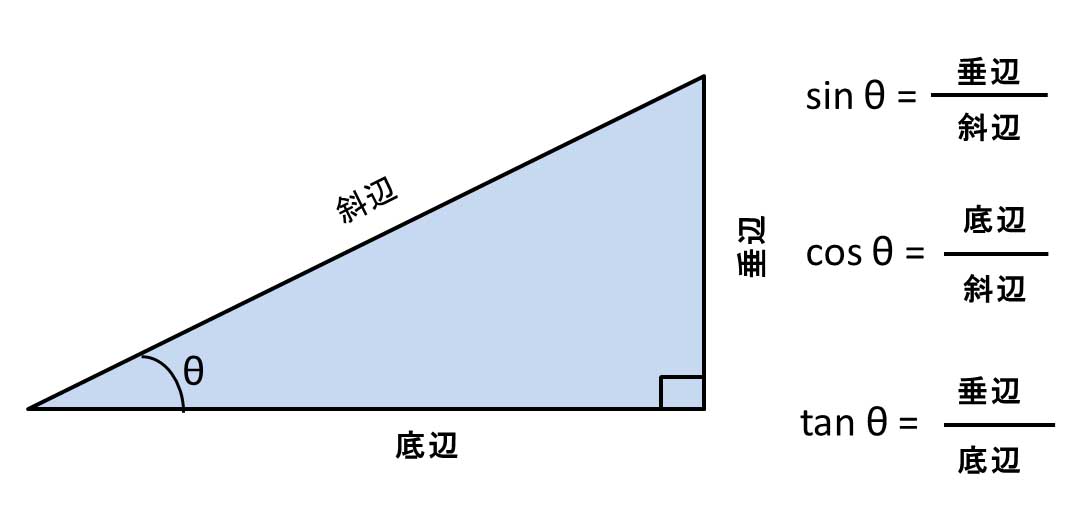
三角関数 三角関数でまずしっかりおさえておきたいのは、やはり sin \sin sin (サイン)、 cos \cos cos (コサイン)、 tan \tan tan (タンジェント) です。 サインとコサインとは何かを覚えるときに、直角三角形の辺の関係だけで覚えていると応用し単位円を使って、一般の角度θについても三角関数を定義できます。 実務で使うなら、上の定義で十分でしょう。 三角関数の使い方1(角度から長さを求める) 例題:50cmのアームの一方を固定して、地面との角度が40°になるまで持ち上げたとき、 高さhを逆三角関数とは 逆三角関数 (inverse trigonometric function) でやることは、その逆です。 値を与えて角度を得ます 。 例えば cos x \cos x cosx に対する逆三角関数である y = arccos x y = \arccos x y = arccosx では、 x = 1 2
S formula (1) S =√s(s−a)(s−b)(s−c), s = (abc) 2 (2) if a≥b,c h = 2S a, B=sin−1 h c, C= sin−1 h b if b≥ c,a h = 2S b, C =sin−1 h a, A=sin−1 h c if c≥ a,b h = 2S c, A= sin−1 h b, B=sin−1 h a (3) ABC = 180 T r i a n g l e u s i n g H e r o n ′ s f o r m u l a ( 1) S = s ( s − a) ( s − b) ( s − c), s = ( a b c) 2 ( 2) i f a ≥ b, c h = 2 S a, B先生のいってることは分かったけど、でも、それは単にa,bの見方を変えただけで、角度θとの深い関係はやっぱり見えないと思うんですけど。 後はコサインが右辺の となる角度を求めて、60°±45°より、15°,105 三角関数の合成公式もその典型的象徴/ 三角関数(度) 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 Right triangle (1) cosθ = a c, sinθ= b c, tanθ= b a (2) P ythagorean theorem a2b2 =c2 R
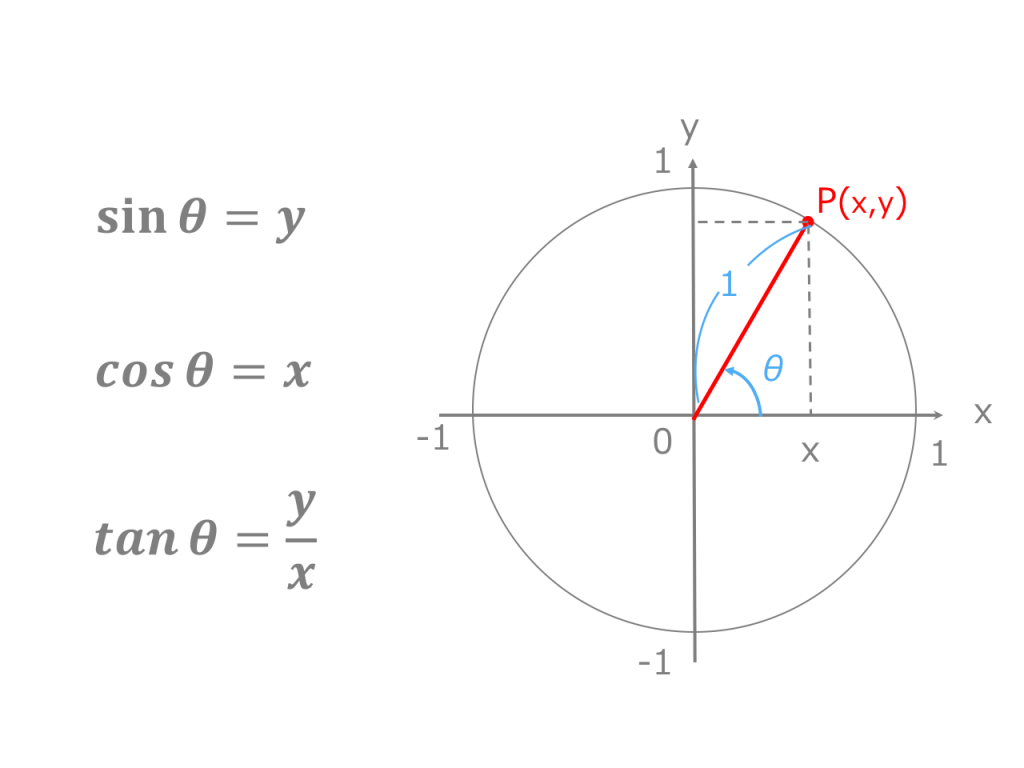
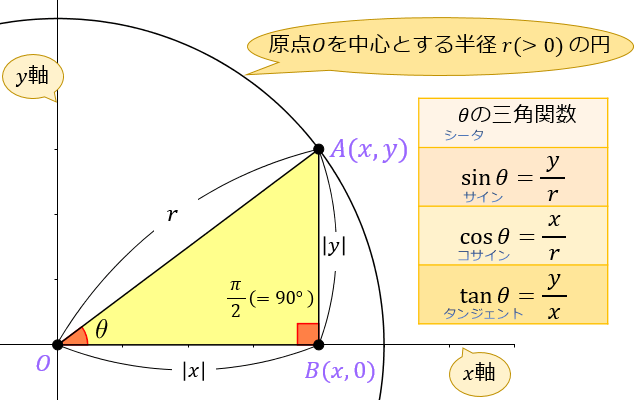
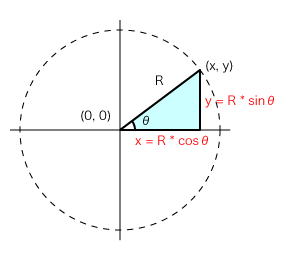
三角関数電卓 |関数電卓|時間計算電卓|三角関数電卓| サイトマップ|ホーム| 三角関数の角度、逆関数、辺の長さから、角度、三角関数値、辺の長さが求められます。 角度は度数指定、ラジアン指・三角関数から角度(逆三角関数) 三角関数から角度(逆三角関数)を計算します。 sin(サイン)から角度 cos(コサイン)から角度 サイン・コサイン・タンジェント まず、原点 O を中心とする 半径 r の円 と、その円上の 点 A (x, y) を考えます。 「 x 軸の正の部分」と線分 O A による(反時計回りを正とする)角の大きさ ∠ B O A = θ に対して



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ




電験三種の数学 逆三角関数を覚える 電験3種ネット
三角関数の必ず覚えなくてはならない5つの性質 ①sin2θcos2θ=1 ② ①、②とも三角関数の定義の単位円を思い出せば、簡単です。 ①は単位円の方程式がX 2 Y 2 =1だから、それにX=cosθ、Y=sinθを代入すれば出来ます。 また、②は だからX=cosθ、Y=sinθを代入三角形を表すとき 多くの場合、頂点の名前は A , B , C の順に左回りに付けます。 辺の名前は「向かい合う角」の小文字で表します。 したがって、 A の対辺 BC を a とします。 同様にして、特に断り書きがなければ b=AC , c=AB になります。 頂点の名前 A , B , C でその内角∠ A 、∠ B 、∠ C の大きさを表し、単に sin A , sin B , sin C などと書きます。 例 右図において 0 はじめに 三角関数について思うこと 三角関数というと高校時代に苦しだ方も多いかもしれません。とにかく公式も多くて、最初のうちは何に使えるのかよくわからない印象を抱きがちです。しかし実際は、理系であればいかなる分野に



三角関数 とは わかりやすくまとめてみた 動画あり もんプロ 問題発見と解決のためのプログラミング




Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews
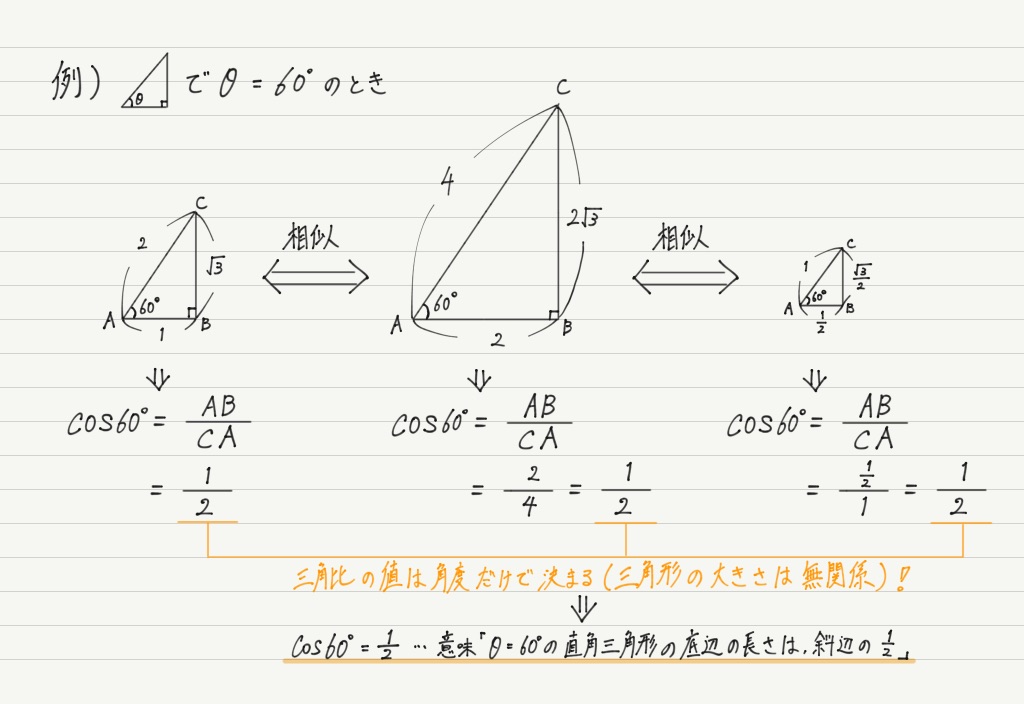
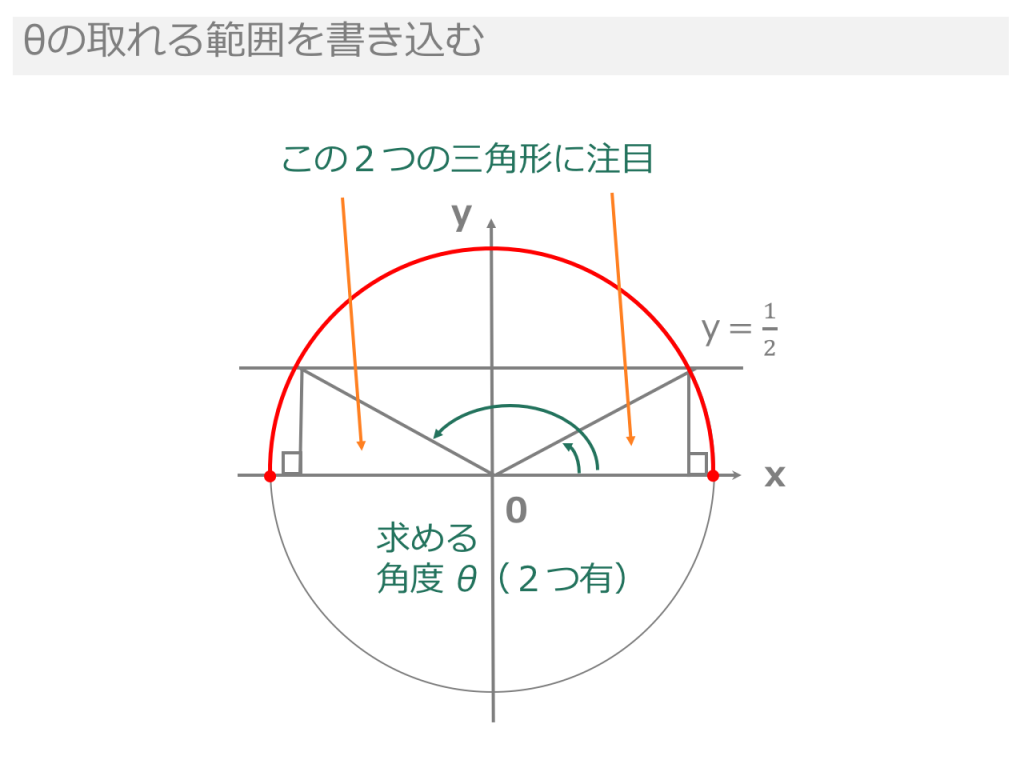
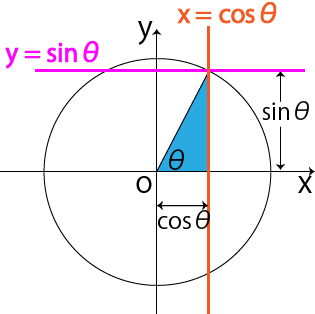
高さと斜辺から角度と底辺を計算 直角三角形の高さと斜辺から傾斜角と底辺を計算します。 三角形の3辺から角度を計算 三角形の3辺の長さから3角の角度を計算します。 三角関数の角度sinを求める②:sinθ=aのときy=aをグラフに書く sinθはy座標であるため、対応させるためにsinθ=aを求めるときはy=aをグラフに書き込みます。 今回は であるので を単位円のグラフに書き込みます。 次に単位円と との交点と原点を直線で結び、交点からx軸に垂線を下ろします。 すると三角形が2つできます。 この三角形は単位円が半径1であることと解説 三角比というのは,与えられた角度に対して,ただ1つ値が決まるもので,その角度が「どんな形の三角形の角の大きさであるか」にはよらないからです。 この話を考えるとき,三角比の 「値を求める」 のか, 「値を利用する」 のかを区別して考えてみましょう。




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト




中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
1 三角関数の定義 動径 が 軸の正の向きをなす角度を とするとき,次の比の値は(相似図形の性質から)半径 の大きさに関係なく,角度 だけで定まる.そこで, の関数になり,三角関数と呼ばれる. 2 三角関数の性質 ※以下においては,角 として第1 基本的に、三角関数の角度は 半径 \(1\) の「単位円」 を利用して求めることができます。 単位円 \(1\) 周分の角度は、度数なら \(\color{red}{360^\circ}\)、ラジアンなら \(\color{red}{2\pi}\) 直角三角形も、単位円も書かない方法なので、時短したいときなどにご活用ください(*˙꒳˙*)‧⁺ ︎* 目次 1、cos、sinの求め方 2、tanの求め方 ⌒⌒⌒⌒⌒⌒ * 必要なもの * ・左手 ・√(指の数) / 2 (こちらは頭の片隅に置いといてください♪



三角関数の角度は 3分でわかる求め方 公式と計算 表との関係



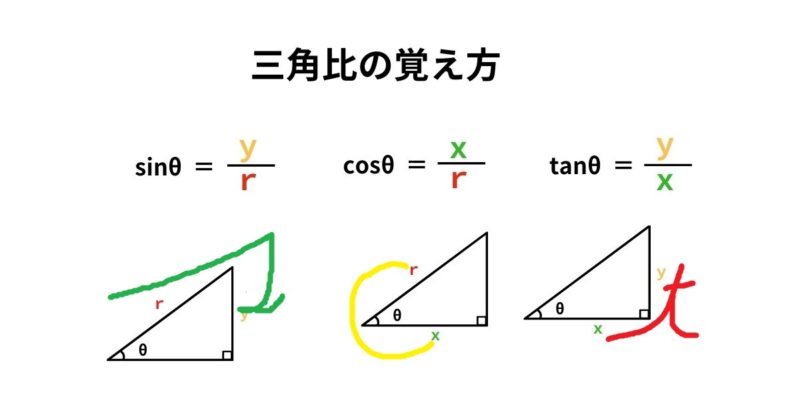
三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ
高校で習う三角関数ですが、当然数学検定でも前提知識として求められます。 三角関数の基本となる、 sin 、 cos 、 tan に関しては求め方と意味をまずは理解しましょう。 そうする事で後々出てくる公式の意味や求め方もスムーズに理解出来るようになります。角度θが90◦以上の場合の三角比を 次で定める。 正の数r に対し,点Q(r,0) を原点 O(0,0) を中心として反時計まわりに角 度θだけ回転した点をP(X,Y) とする。 このとき角度θにおける三角比を sinθ= Y r, cosθ= X r, tanθ= Y X で定める。 こんにちは。 da Vinch (@mathsouko_vinch)です。 三角関数においてある角度の三角比を「覚える」のはナンセンスです。なぜなら三角関数では角度はいくらでも大きく、またマイナスの角度も考えられますから。さらに私たちがち




三角形の角度を求める問題 小学生 中学生の勉強



1
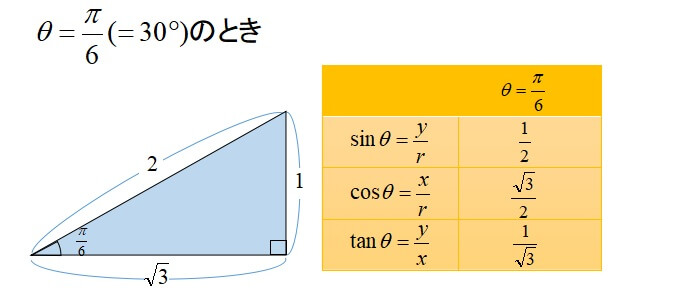
角度にθ[°]を使用した場合、三角関数を用いて以下のような関係式が成り立ちます。 三角関数のtanθ=高さ/底辺 で求めることができるため、 タンジェントの逆関数であるtan1 を使用するとθ=tan1 (高さ/底辺)と計算できるのです。解説 ≪三角比の値の求め方≫ sinθ,cosθ,tanθの値は,次の「よく出る2つの三角形」と「sinθ,cosθ,tanθの定義」を覚えていれば導けます。 これらを使った求め方 ①θの値(角度)を見て,「よく出る2つの三角形」のうち,当てはまる三角形をかき出す。/ 三角関数(度) 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 Right triangle (1) cosθ = a c, sinθ= b c, tanθ= b a (2) P ythagorean theorem a2b2 =c2 R i g h t t r i a n g l



Windows電卓で三角関数を計算する方法 Trismegistuslabo トリメギブログ




三角比と三角関数 高校物理をあきらめる前に 高校物理をあきらめる前に
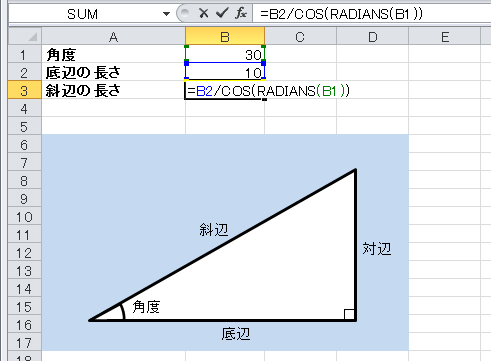
角度が30度の場合のcos,sin,tanを求めてみましょう。 度数を直接使うには、RADINA関数を使ってラジアンに直して計算します。 sin,cosカーブを書いてみます セルに「0」と入力します。直角三角形の高 直角三角形の高さを求めるための式 さを求めたい 「=11*SIN(RADIANS (36))」と入力 三角関数とは逆に「辺の長さから角度を求める」には、逆三角関数を使い ます。逆三角関数にはアークサイン(arcsin、逆正弦)、アークコサイン ここでは、角度から三角関数の値を求めたり、三角関数の値から角度を求める問題を見ていきます。 角度から三角関数の値を求める 例題1 次の値を求めなさい。 (1) $ sin dfrac{7}{6} pi$ (2) $




関数電卓の使い方 三角関数 Itよろず雑記帳



三角関数の合成とは 公式 証明 最大最小や範囲の問題 受験辞典




高校数学 三角比からの角度の求め方3 Tan8 映像授業のtry It トライイット



2点間の距離を測ろう 三角関数 Gameworks Lab



角度 の 求め 方 ニュース ニュース




Excel 三角関数と逆三角関数で 三角形の辺の長さや角度を求める方法まとめ わえなび ワード エクセル問題集




角度の求め方 算数の教え上手 学びの場 Com




三角関数の公式の一覧 Wikipedia



工業用 三角関数計算ツール




三角形の辺から角度を計算 製品設計知識




Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews




タンジェントとは何か 中学生でも分かる三角関数の基礎
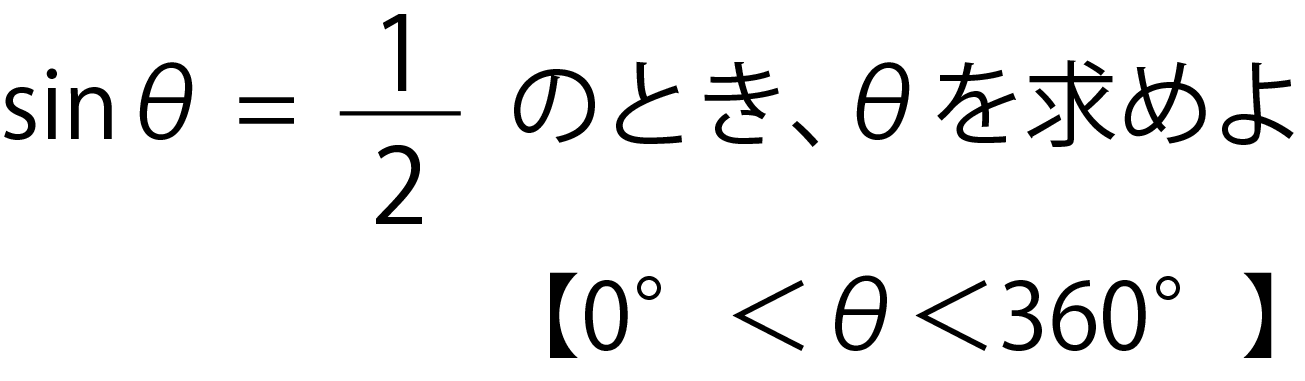



三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ



図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に




三角関数の知識 やさしい電気回路
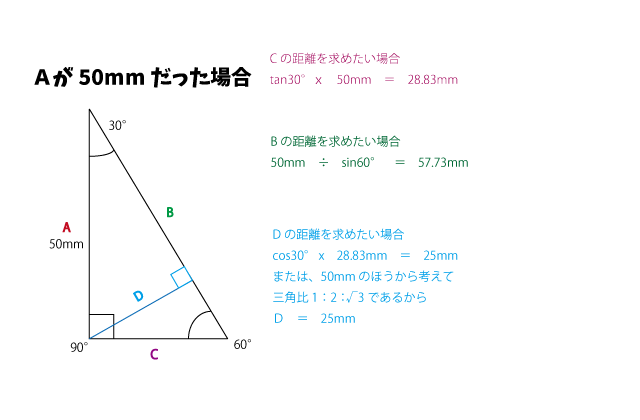



射出成形金型 三角関数編 関数電卓を使った困ったときの計算方法




三角関数を使った測量士補試験の計算問題 中山祐介の土地家屋調査士 測量士補 合格 ブログ



三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ



2



三角形の角度を求める 思考力を鍛える数学




高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト
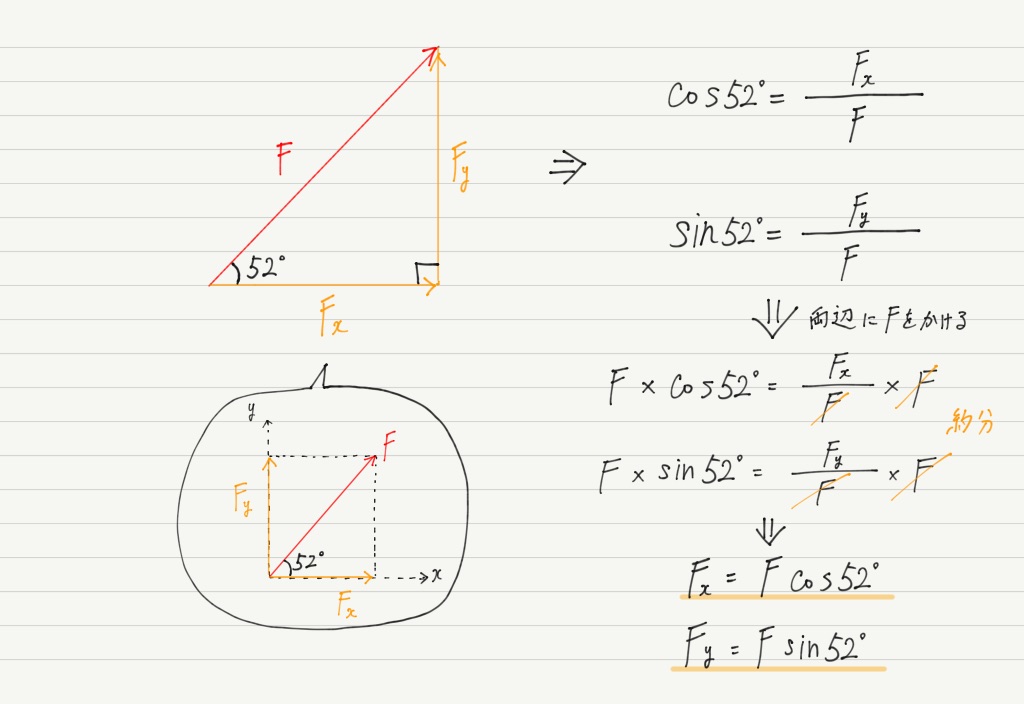



力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に
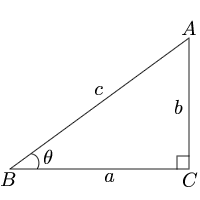



三角関数から角度 逆三角関数 三角形の計算 計算サイト
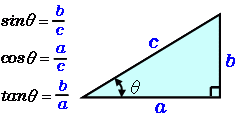



三角関数 度 高精度計算サイト




三角比 三角関数の基礎sin Cos Tanが簡単に分かる解説 Rikeinvest




わかりやすい三角比と基本公式 Irohabook




三角関数の知識 やさしい電気回路
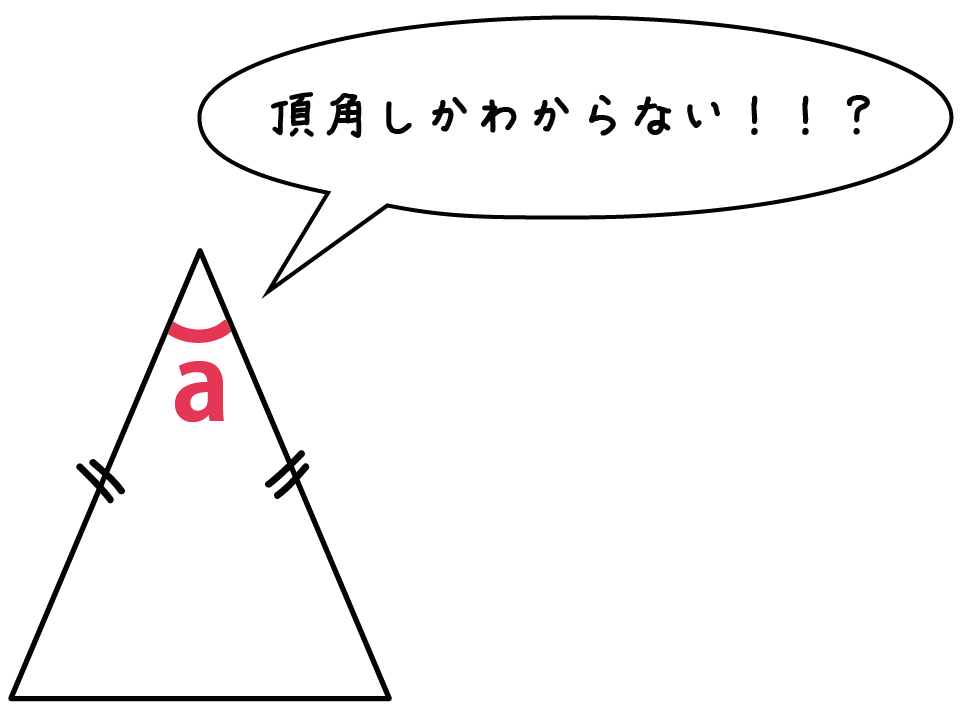



簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく




三角関数の合成公式 証明 問題 Cos型について 理系ラボ



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ



三角関数の角度は 3分でわかる求め方 公式と計算 表との関係



三角関数をマスターしよう その2 金属加工 ものづくり初心者のメモ帳 Mc マシニングセンター Ncプログラムの学習




有名角 準有名角のsin Cosの値 一覧 理系のための備忘録
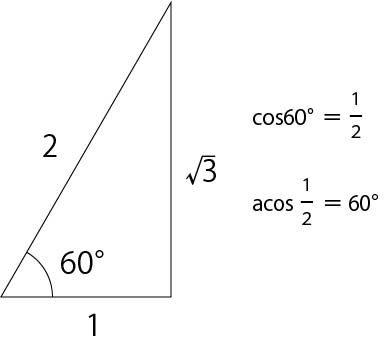



Excelで三角関数の計算 Acos関数を使ってみよう パソコンスキルと資格のscワンポイント講座




三角関数は何に使えるのか サイン コサイン タンジェントの活躍 Qiita
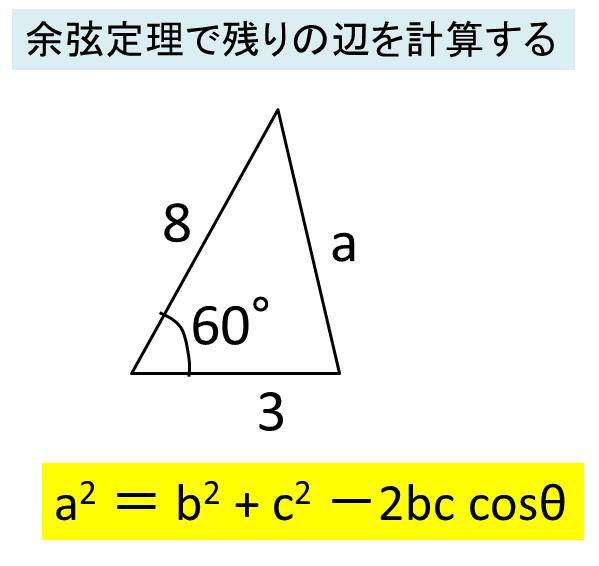



Excel エクセルで余弦定理の計算をする方法 角度や辺の長さを求める




Javaでmathクラスを使って三角関数を求める方法を現役エンジニアが解説 初心者向け Techacademyマガジン



日曜大工で使う数式




三角関数で角度から座標を導くふたつの式の使い途 Qiita




三角関数
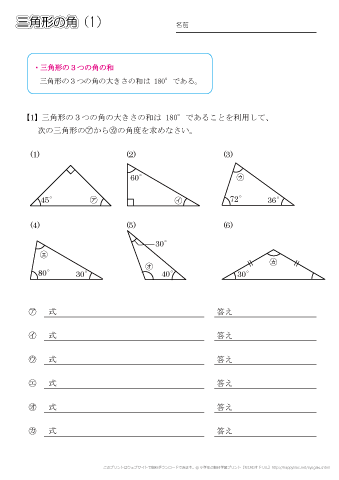



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生



三角関数について




余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ




角度の求め方 角度の求め方 Mqttk




角度の場合分けについて 数学 苦手解決q A 進研ゼミ高校講座
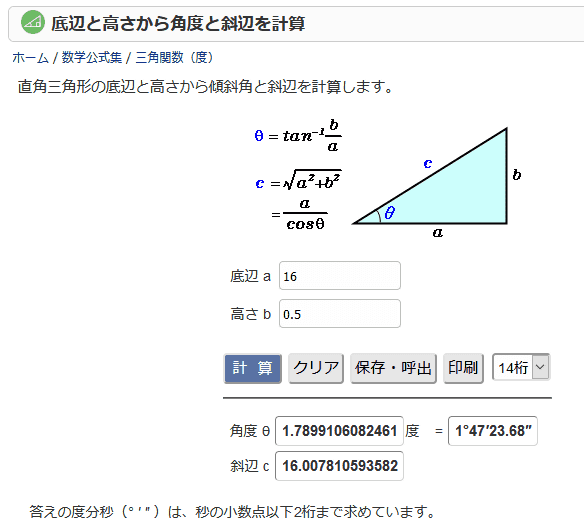



表計算ソフトを使って 底辺 と 高さ から 角度 を求める




タンジェントとは何か 中学生でも分かる三角関数の基礎



Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau




高校数学 数 76 三角比 基本編 Youtube




余弦定理で角度を求める方法 数学の星




Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算




高校数学 三角比からの角度の求め方1 Sin8 映像授業のtry It トライイット
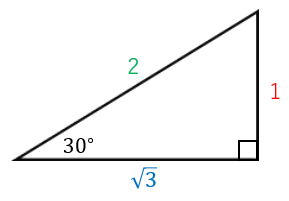



30度 45度 60度のsin Cos Tan 具体例で学ぶ数学



1
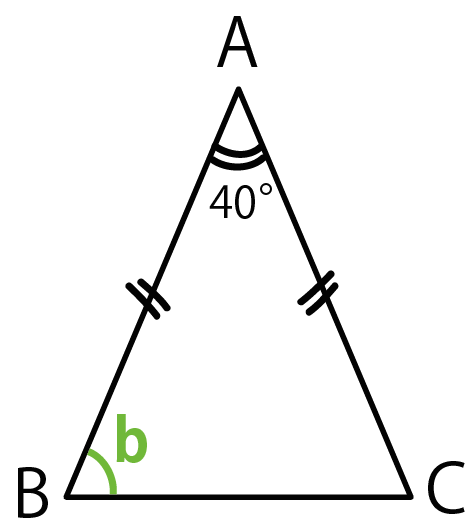



簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく




三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com



三角関数 1 Cg 数学 06aa




三角形の3辺から角度を計算 高精度計算サイト




家電やスマホに必須 三角関数は陰の働き者 中高数学おさらい 三角関数 数列 文系でも怖くない 学び直し 数学 ダイヤモンド オンライン
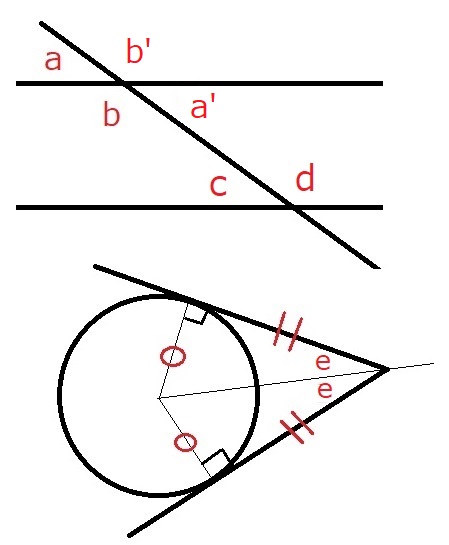



三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ
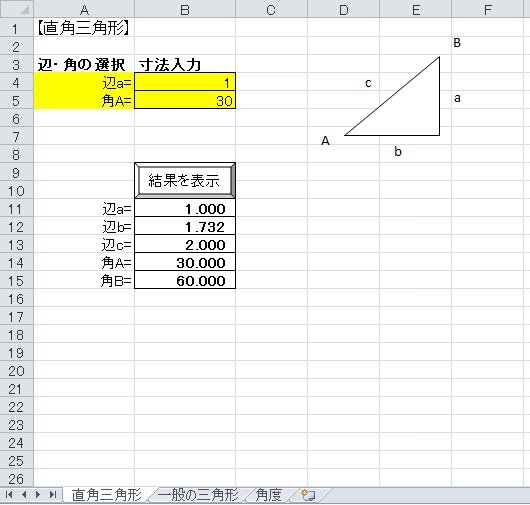



エクセル 三角関数計算 S Project



3
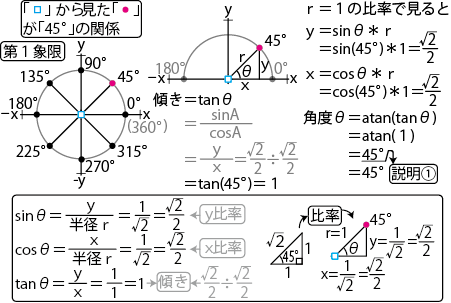



1研究中 C 数学1 三角関数 1 逆三角関数 三角比 ラジアン Sin Cos Tan Asin Acos Atan Atan2



上級 三角関数 Shade3d チュートリアル




三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ




直角三角形の辺を求める Youtube



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典



角度と底辺から斜辺と高さを計算 高精度計算サイト




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月



角度からコサインを計算するには Cos Radiansの解説 エクセル関数リファレンス




サインコサインタンジェント Sin Cos Tan とは何を表す 良い覚え方を紹介 遊ぶ数学




三角関数の基礎知識



エクセルのグラフで学ぶ気象学0001




三角関数は何に使えるのか サイン コサイン タンジェントの活躍 Qiita




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



三角関数 ncプログラム基礎知識



サイン コサイン タンジェントの角度の求め方 一歩一歩ぐんぐんブログ




直角三角形の角度の求めかたは 直角三角形の残りの角度を求める 数学 教えて Goo




三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す



三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座



Vba 三角比をもとめる Sin関数 Cos関数 Tan関数 角度をもとめる Atn関数



三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ




底辺と高さから角度と斜辺を計算 高精度計算サイト



4 2 三角関数 Yasushi Noguchi Class
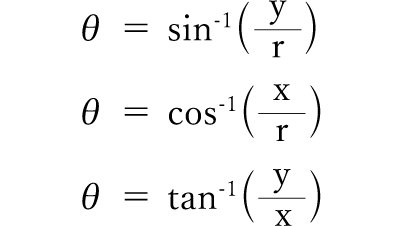



三角関数をマスターしよう その3 金属加工 ものづくり初心者のメモ帳 Mc マシニングセンター Ncプログラムの学習



三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com



高1数学 木の高さを三角比を用いて求める方法を解説 数スタ




小5 算数 小5 31 三角形の角 Youtube
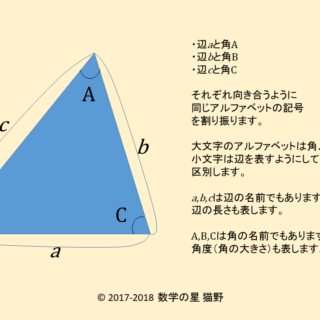



第2余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星




力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に


コメント
コメントを投稿